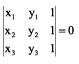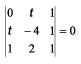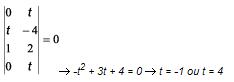Blog do Prof. Francisco Rêgo
Acompanhe o blog para aprender um pouco mais de matemática!
quinta-feira, 16 de setembro de 2010
Cálculo das funções trigonometricas
Fazendo uma pesquisar na internet encontrei esse site ,muito importante e interessante para nosso estudo sobre trigonometria .
http://ecalculo.if.usp.br/funcoes/trigonometricas/circunferencia/circunf_orient.htm
http://ecalculo.if.usp.br/funcoes/trigonometricas/circunferencia/circunf_orient.htm
CIRCUNFERÊNCIA TRIGONOMÉTRICA
Se α = 0, P coincide com A.
Se α > 0, o sentido do círculo trigonométrico será anti-horário.
Se α < 0, o sentido do círculo será horário.
O comprimento do arco AP será o módulo de α.
.jpg)
Na ilustração a seguir estão visualizados alguns números importantes, eles são referenciais para a determinação principal de arcos trigonométricos:
.jpg)
Por exemplo, para localizarmos 8π/3 = 480º, damos uma volta completa no sentido anti-horário e localizamos o arco de comprimento 2π/3, pois 8π/3 = 6π/3 + 2π/3 = 2π + 2π/3.
.jpg)
Na localização da determinação principal de –17π/6 = –510º, devemos dar 2 voltas completas no sentido horário e localizarmos o arco de comprimento –5π/6, pois –17π/6 = –12π/6 – 5π/6 = 2π – 5π/6.
.jpg)
Equipe Brasil Escola
sábado, 11 de setembro de 2010
Geometria Analitica
Coordenadas do Baricentro de um Triângulo
Aplicação
Calcule as coordenadas do ponto médio M do segmento , sendo A (6, 10) e B(2, 8).
Solução:
Xm = 3 + 5 = 8 = 4 Ym = 11 + 7 = 18 = 9
2 2 2 2
Resposta: M (4, 9)
COORDENADAS DO BARICENTRO DE UM TRIÂNGULO
Baricentro de um triângulo ao ponto G é a intersecção das três medianas deste triângulo.
Mediana de um triângulo é um segmento de reta que sai de um vértice e divide o lado oposto a este em duas partes iguais.
A abscissa e a ordenada do baricentro de um triângulo ABC é igual a média aritmética das abscissas e ordenadas, respectivamente, de seus vértices.
xg = xa + xb + xc Xg = Ya + Yb + Yc
3 3
Aplicação
Seja um triângulo cujos vértices são A (5, 4), B (5, 7), C (8, 4); calcule as coordenadas do baricentro.
Solução:
Xg = 5 + 5 + 8 = 18 = 6 Yg = 4 + 7 + 4 = 15 = 5
3 3 3 3
Resposta: G (6, 5)
PONTOS COLINEARES
Sejam A(x1, y1), B(x2, y2) e C(x3, y3) três pontos do plano cartesiano. A condição necessária e suficiente para que os três pontos estejam juntos na mesma reta (alinhados) é que:
Para que A, B e C estejam alinhados devemos ter:
Observação: Para pontos não colineares (vértices de um triângulo, por exemplo), devemos ter a mesma matriz mostrada anteriormente, mas diferente de zero.
Aplicação
Calcule as coordenadas do ponto médio M do segmento , sendo A (6, 10) e B(2, 8).
Solução:
Xm = 3 + 5 = 8 = 4 Ym = 11 + 7 = 18 = 9
2 2 2 2
Resposta: M (4, 9)
COORDENADAS DO BARICENTRO DE UM TRIÂNGULO
Baricentro de um triângulo ao ponto G é a intersecção das três medianas deste triângulo.
Mediana de um triângulo é um segmento de reta que sai de um vértice e divide o lado oposto a este em duas partes iguais.
A abscissa e a ordenada do baricentro de um triângulo ABC é igual a média aritmética das abscissas e ordenadas, respectivamente, de seus vértices.
xg = xa + xb + xc Xg = Ya + Yb + Yc
3 3
Aplicação
Seja um triângulo cujos vértices são A (5, 4), B (5, 7), C (8, 4); calcule as coordenadas do baricentro.
Solução:
Xg = 5 + 5 + 8 = 18 = 6 Yg = 4 + 7 + 4 = 15 = 5
3 3 3 3
Resposta: G (6, 5)
PONTOS COLINEARES
Sejam A(x1, y1), B(x2, y2) e C(x3, y3) três pontos do plano cartesiano. A condição necessária e suficiente para que os três pontos estejam juntos na mesma reta (alinhados) é que:
Aplicação :
Determinar o valor de t para que os pontos A (0, t), B (t, - 4), C (1, 2) estejam alinhados.
Solução: Para que A, B e C estejam alinhados devemos ter:
Resolvendo-se o determinante e eliminando-se a última coluna e repetindo a primeira linha no fim, formando uma quarta linha, temos:
Observação: Para pontos não colineares (vértices de um triângulo, por exemplo), devemos ter a mesma matriz mostrada anteriormente, mas diferente de zero.
Relações Trigonometricas
As relações entre os valores das funções trigonométricas de um mesmo arco são denominadas relações trigonométricas.
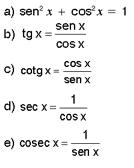
Observações:
a) cotg x = co-tangente de x
b) sec x = secante de x
c) cosec x = co-ssecante de x
Aplicação
Simplificar a expressão:
1 – sen x . cos x . tg

Aplicação
Calcular sen 75°.
Solução:
Podemos observar que 75º = 30º + 45º; logo sen 75º = sen (30º + 45º). A partir da fórmula, temos:
sen (30º + 45º) = sen 30º. cos 45º + sen 45º . cos 30º =
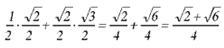
Fonte : colégio WEB
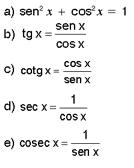
Observações:
a) cotg x = co-tangente de x
b) sec x = secante de x
c) cosec x = co-ssecante de x
Aplicação
Simplificar a expressão:
1 – sen x . cos x . tg

Aplicação
Calcular sen 75°.
Solução:
Podemos observar que 75º = 30º + 45º; logo sen 75º = sen (30º + 45º). A partir da fórmula, temos:
sen (30º + 45º) = sen 30º. cos 45º + sen 45º . cos 30º =
Fonte : colégio WEB
Assinar:
Comentários (Atom)