Aplicação
Calcule as coordenadas do ponto médio M do segmento , sendo A (6, 10) e B(2, 8).
Solução:
Xm = 3 + 5 = 8 = 4 Ym = 11 + 7 = 18 = 9
2 2 2 2
Resposta: M (4, 9)
COORDENADAS DO BARICENTRO DE UM TRIÂNGULO
Baricentro de um triângulo ao ponto G é a intersecção das três medianas deste triângulo.
Mediana de um triângulo é um segmento de reta que sai de um vértice e divide o lado oposto a este em duas partes iguais.
A abscissa e a ordenada do baricentro de um triângulo ABC é igual a média aritmética das abscissas e ordenadas, respectivamente, de seus vértices.
xg = xa + xb + xc Xg = Ya + Yb + Yc
3 3
Aplicação
Seja um triângulo cujos vértices são A (5, 4), B (5, 7), C (8, 4); calcule as coordenadas do baricentro.
Solução:
Xg = 5 + 5 + 8 = 18 = 6 Yg = 4 + 7 + 4 = 15 = 5
3 3 3 3
Resposta: G (6, 5)
PONTOS COLINEARES
Sejam A(x1, y1), B(x2, y2) e C(x3, y3) três pontos do plano cartesiano. A condição necessária e suficiente para que os três pontos estejam juntos na mesma reta (alinhados) é que:
Aplicação :
Determinar o valor de t para que os pontos A (0, t), B (t, - 4), C (1, 2) estejam alinhados.
Solução: Para que A, B e C estejam alinhados devemos ter:
Resolvendo-se o determinante e eliminando-se a última coluna e repetindo a primeira linha no fim, formando uma quarta linha, temos:
Observação: Para pontos não colineares (vértices de um triângulo, por exemplo), devemos ter a mesma matriz mostrada anteriormente, mas diferente de zero.
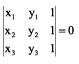
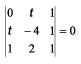
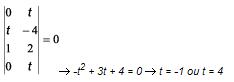
Nenhum comentário:
Postar um comentário